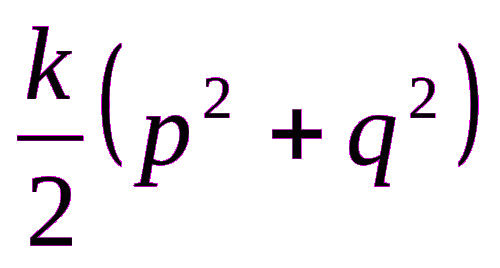Математик из Бристольского университета нашел решение части 64 – летней математической задачи. Он выразил число 33 как сумму трех кубов.
С 1950-х годов математики задавались вопросом, могут ли все целые числа быть выражены как сумма трех кубов; всегда ли уравнение k = x3+ y3+ z3 имеет решение.
Головоломка представляет собой диофантово уравнение в области теории чисел и является частью одной из самых загадочных и коварно трудных задач математики. Ответ до сих пор неизвестен.
Поскольку вычислительная мощность увеличилась, было выявлено больше вариантов решений, а также группа, которая, как известно, не имеет решений; те, которые оставляют остаток 4 или 5 при делении на 9. До недавнего времени оставалось только два неизвестных решения под 100; 33 и 42.
Доктор Эндрю Букер из математической школы Университета обнаружил решение для числа 33: (8,866,128,975,287,528)3 + (-8,778,405,442,862,239)3 + (-2,736,111,468,807,040)3.
Доктор Букер рассчитывал провести более тщательный поиск, но через пару недель компьютер нашел решение.
По его словам, у него было довольно хорошее предположение, что ему удастся найти что-то для одного из чисел ниже 1000. Но он не знал, что это будет число 33.
Как говорит Букер, мы не знаем, имеют ли оставшиеся числа бесконечно много решений. Это довольно загадочно.
Исторически сложилось так, что решения для некоторых из этих чисел не существовало, их было невозможно решить.
Математики просто не знают, смогут ли они когда-нибудь ответить на это для каждого числа. Может быть, проблема суммы трех кубов неразрешима или независима от аксиом математики.
Но каждое новое открытие дает доказательство современной гипотезы о том, что все подходящие числа имеют решения.
Как считает ученый, это как раз на границе между тем, что мы знаем, как доказать, и тем, что, как мы подозреваем, может оказаться неразрешимым.