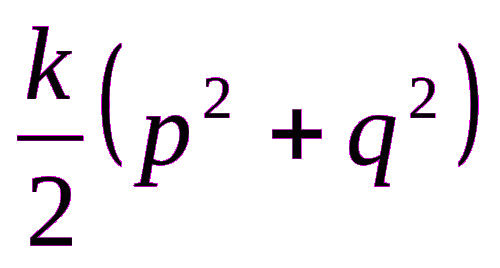Умножение 2 x 2 легко. Но умножение двух чисел с более чем миллиард цифрами каждый требует серьезных вычислений.
Ученые утверждают, что достигли максимального предела скорости умножения, впервые предложенного почти 50 лет назад. Это может оказаться самым быстрым возможным способом умножения целых чисел.
При выполнении вычислений с непомерно большими числами наиболее важной мерой скорости является время, необходимое для выполнения вычисления, оно растет по мере умножения длинных строк цифр.
Этот рост выражается через n, определяемый как число цифр в умножаемых числах. Для нового метода количество требуемых операций пропорционально n раз логарифму n, выраженному как O (N log n) в математическом lingo
Это означает, что если удвоить количество цифр, то количество требуемых операций увеличится немного быстрее, более чем в два раза больше времени, которое требуется для расчета.
Ранее предсказанная максимальная скорость для умножения была O (N log n), что означает, что новый результат соответствует ожидаемому пределу.
В новом исследовании ученые рассматривали только цифры с более чем 10 214857091104455251940635045059417341952 при записи в двоичном формате, в котором числа кодируются с последовательностью 0s и 1s. Но ученые на самом деле не выполняли ни одного из этих массивных умножений, потому что это намного больше цифр, чем количество атомов во Вселенной.
Это означает, что на компьютере нет способа делать такие вычисления, потому что атомов не достаточно, чтобы даже представлять такие огромные числа, а тем более умножать их вместе.
Даже если метод не является широко полезным, достижение прогресса в решении такой фундаментальной проблемы, как умножение, по-прежнему является великим достижением.